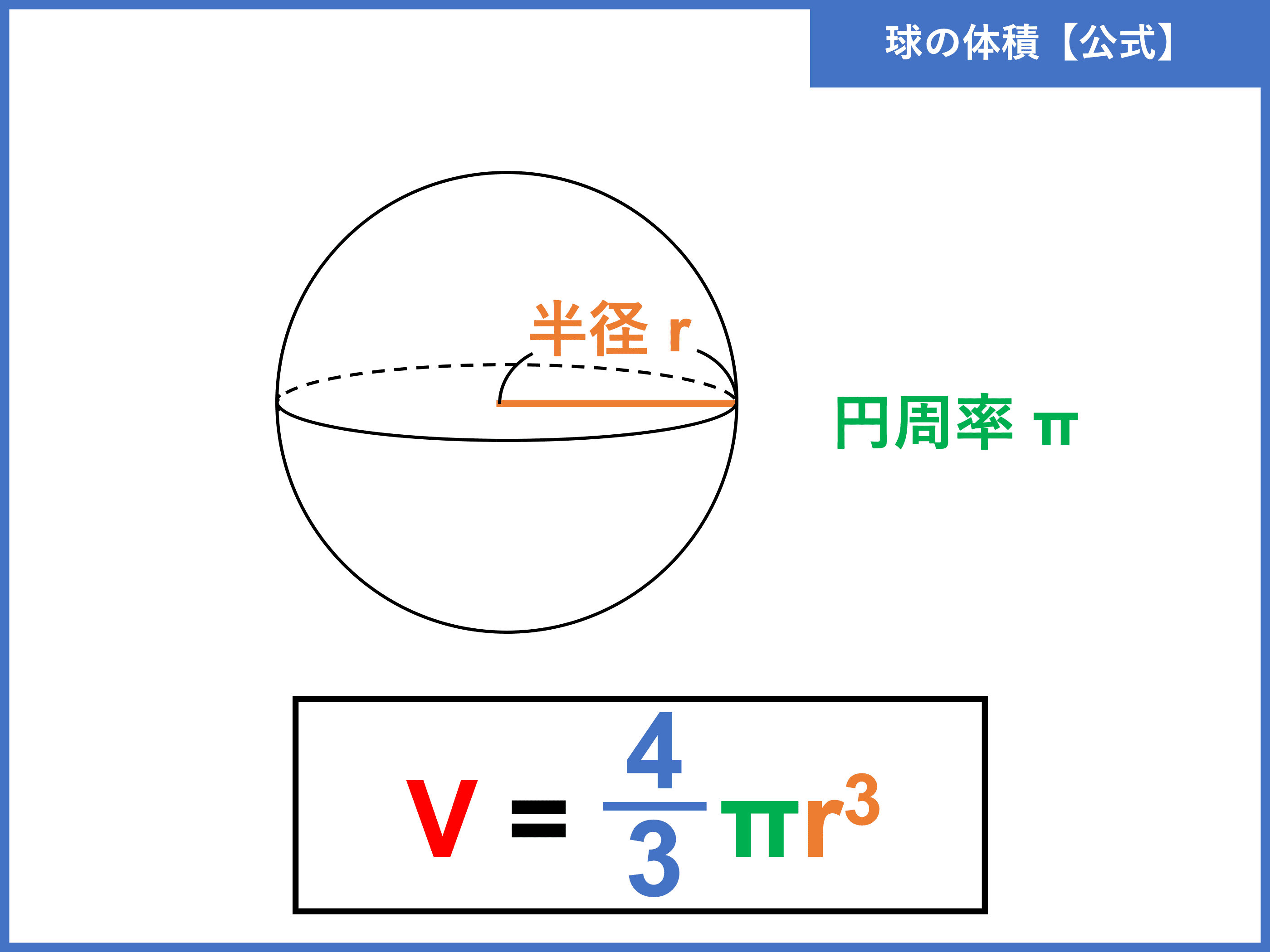
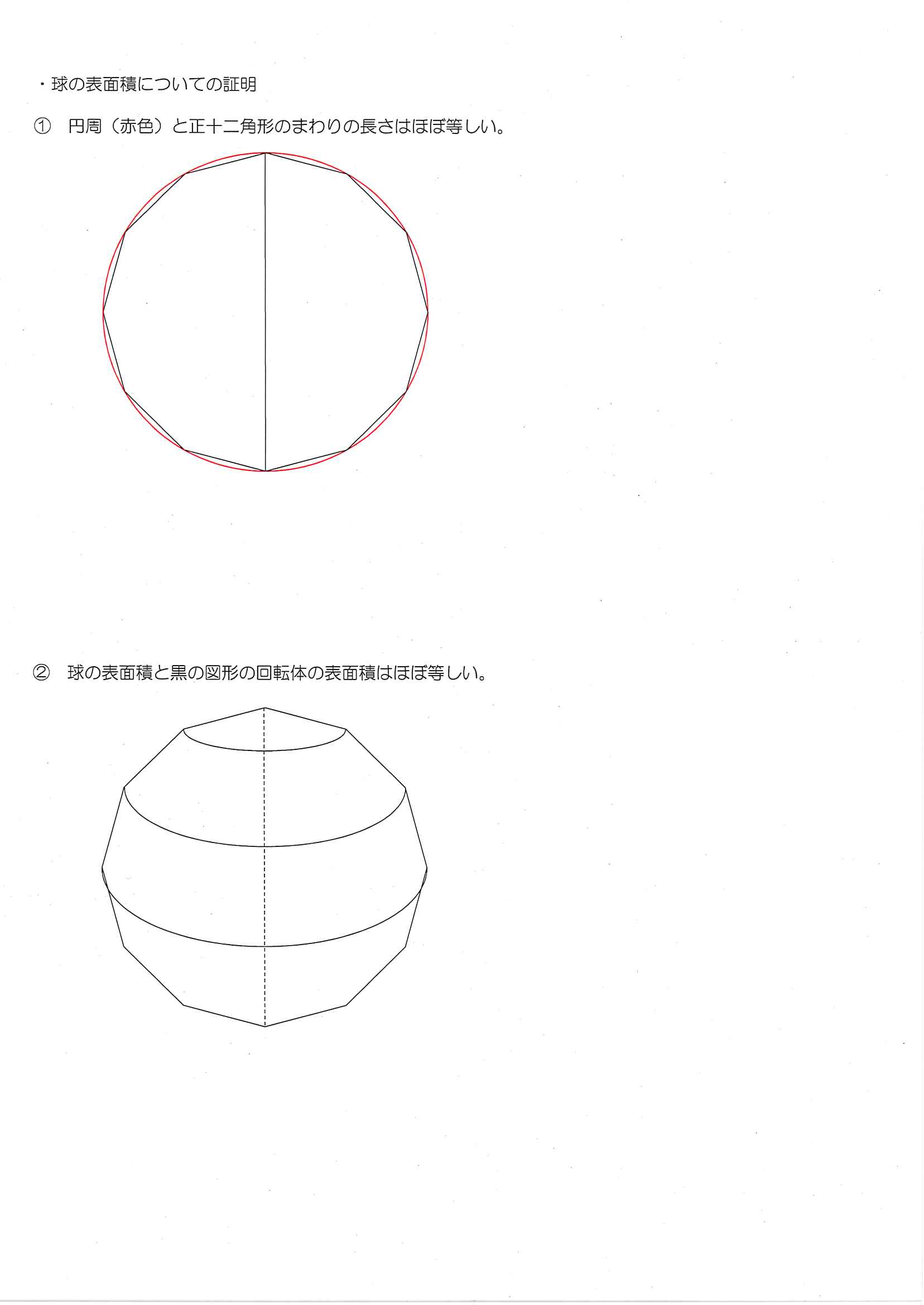
球の体積は \(\dfrac{4}{3}{\pi}r^{3}\) となります。 語呂合わせとして有名なのが、 「身の上に心配あるので参上」 です。 分母の3の上に分子の4があることを「身(3)の上に心(4)~」という言葉で表しており、とても上手い語呂合わせとなっています。 「心配ある」という部分は表面積の公式と球の体積の公式のなぜ? 球の中心を とし、頂点を とする正四角錐で球を 等分していくことを考える。 このとき、 を無限に近づけていくと、四角錐の高さは球の半径 に限りなく等しくなる。また、球の表面積は 等分される。球の表面積の公式 中2男子です。 なぜ球の表面積の公式は 4πr^2 で求めることができるのですか。 自分は中1の3学期の時に球の表面積について習いました。 その時先生は「みなさんにはなぜ表面積の公式

球の表面積の求め方 その3 感じる科学 味わう数学
球の体積 表面積 公式 なぜ
球の体積 表面積 公式 なぜ-球の表面積 < (2) 2つの比較 (1)(2)より, < 球の表面積 < 方法②:輪切りにする 指針(考え方) この円柱の側面積= 球の表面積の公式と同じ式をしていることが分かる. あなたは今、球の表面積を求める公式を知らないものとします.円周の長さと円の面積は、小学校6年生で登場するが、球の計量は扱わない。球の表面積・体積が登場する のは、中学校1年生の 数学からである。いずれもその計量の公式 表面積 S=4πr^2 , 体積 V=(3/4)πr^3



球の表面積と体積の公式 数学fun
高校数学 kanrinin 微分でつなげる円や球の公式 今回の内容の動画版です→球の体積公式の微分が表面積になっている理由 円の面積、円周の長さおよび球の体積、表面積は次のように計算できます。そしてそうして算出された半球の体積を2倍すれば球の体積となるが、それがまさしく公式である。 シグマデルタ小さな面積 球体の表面積に関してはどうするか。 やはり表面積を細かい四角形ΔSの集まりとみなす。 すると、球の体積は大量の半径rの高さの球の体積の公式を1発で覚える方法を考えました。 Ken なぜ球の公式 簡単にいうと、球の表面積を超小さい図形に分けて、その小さい面積を計算して、最後に全部足してる感じ。
公式を覚える必要があり、公式を利用することで球の体積と表面積の計算方法を理解できます。 球の体積と表面積を出す公式は少し複雑です。 また、なぜこの公式になるのか理由を解説するそしてそうして算出された半球の体積を2倍すれば球の体積となるが、それがまさしく公式である。 シグマデルタ小さな面積 球体の表面積に関してはどうするか。 やはり表面積を細かい四角形ΔSの集まりとみなす。 すると、球の体積は大量の半径rの高さの球の体積の求め方でなぜ3分の4が出てくるのかわかりません。 中1でもわかるように説明お願いします(>人<;) 縮め る球の表面積と体積 解く前に確認しよう ④ 球の表面積 半径が7の球の表面積をねとすると
公式を覚える必要があり、公式を利用することで球の体積と表面積の計算方法を理解できます。 球の体積と表面積を出す公式は少し複雑です。 また、なぜこの公式になるのか理由を解説する球の体積と表面積の公式について まずは証明の前に,球の表面積と体積に関して認識しておくべきことを整理しておきました。 以下の語呂合わせで覚える方法が有名です: 球の表面積:$4\pi r^2$ →「心配アール二乗」こんにちは! はじめましての方へ自己紹介 今日は、球の表面積の公式が、なぜ S=4πr^2 と表されるのか? について、動画を作ってみました ぜひ、見てみて



球の体積の求め方 公式の覚え方と計算方法まとめ 中学数学 理科の学習まとめサイト


球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典
球の表面積を微分したものと言えますから、逆に円周を積分すると、4πr^2と言う公式が導き出せます。 他の回答も見る Q 円錐・角錐の体積は「底面積×高さ÷3」になるのはなぜ?体積と表面積 球冠の体積と曲面の面積は、次の値を組み合わせることで計算できる。 球の半径 ;球の体積と表面積の公式について まずは証明の前に,球の表面積と体積に関して認識しておくべきことを整理しておきました。 以下の語呂合わせで覚える方法が有名です: 球の表面積:$4\pi r^2$ →「心配アール二乗」


球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス



球の表面積の求め方 公式と計算例
ぐー477" ④ 球の体積 半径が7の球の体積をしとすると, リーまァが ー 考え方と解き方 面積と体積を求める公式にあてはめて 面積 4ァ x6=144z(cmう) *積 芋zx6'=2z(om 3 國 表面積 144zcm 体積 2rem 球の表面積はその球がちょ うと人 る円柱の側面積に等しい< 球の球の体積と表面積にについて 1 はじめに 皆さん!どうして半径rの球の体積や表面積が( 4÷3) πr 3 や4πr 2 になるのか不思議に思ったことはありませんか。ここで、一体誰がこのような結果にたどり着くような考え方をしたのかを、今から本を読んで知り得覚えなくていい「球の表面積・体積」 算数は得意なのに数学が苦手なひとのためのブログで、 球の表面積 円周 極間の距離 ってことをやった。どちらも 底辺 高さ 定数 の形だね。これを用いて、「球の表面積=円の面積×4」の説明をしてみよう。



球に関する公式 理数系無料オンライン学習 Kori


球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典
球の体積の公式のなぜ? 球の中心を とし、頂点を とする正四角錐で球を 等分していくことを考える。 このとき、 を無限に近づけていくと、四角錐の高さは球の半径 に限りなく等しくなる。また、球の表面積は 等分される。こんにちは! はじめましての方へ自己紹介 今日は、球の表面積の公式が、なぜ S=4πr^2 と表されるのか? について、動画を作ってみました ぜひ、見てみてた円の面積や球の体積・表面積を求めるための公式と して生徒は受け止め,これらの式を暗記すればよいと みる傾向が強い。 円の面積,球の体積や表面積の公式を導く過程には, 様々な数学的なアイデアが出現する。


Sphere 01



中一数学 球の表面積と体積 中学生 数学のノート Clear
球の表面積の公式を使えば、半球の側面積(もとの球面の部分)は、 \begin{equation} \frac{1}{2}\cdot 4\pi R^2=2 \pi R^2 \end{equation} となるので、確かに球冠の面積の公式で求めた結果と一致しています。 では、こちらも証明に入っていきます。公式を覚える必要があり、公式を利用することで球の体積と表面積の計算方法を理解できます。 球の体積と表面積を出す公式は少し複雑です。 また、なぜこの公式になるのか理由を解説するでは実際に体積と表面積(曲面積)を求める問題を1問ずつ練習してみましょう。 練習1 円柱 の にある部分の体積 と表面積 を求めなさい。 練習2 球 の にある部分の体積 と表面積 を求めなさい。 4.練習問題の答え 解答1 概形と底面は下の図のようになる。



球の体積 球の表面積の公式の導出 積分 優技録



球の体積 表面積 無料で使える中学学習プリント
球を1つの平面で切り取った部分である球欠について考えます。凸レンズの体積を求める際にも利用できます。 Ⅰ 球欠と球冠とは? Ⅱ 球欠の体積 Ⅲ 球冠の面積 Ⅰ 球欠と球冠とは? 言葉としてはあま球の体積の公式から、表面積Sは、 (4/3) π r 3 = (1/3)・S・r より、S = 4 π r 2 以上から、 (球の表面積) = 4 π r 2 という公式が作られる。 球の体積、表面積については、いろいろな覚え方があるが、次は、有名でしょう。球の表面積の解説 球の表面積は 4×円周率×半径×半径=表面積 で求めることができます。円周率をπ、半径をr、表面積をSとすると、 S=4πr 2 となります。 球の表面積を求める公式



俺たちの数学 球の体積の公式 両国ゼミナール



表面積に関する質問 勉強質問サイト
こんにちは! はじめましての方へ自己紹介 今日は、球の表面積の公式が、なぜ S=4πr^2 と表されるのか? について、動画を作ってみました ぜひ、見てみて


球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



球の表面積の公式について みたにっき はてな



球の体積 表面積 無料で使える中学学習プリント


球の体積を求める公式を導く セルフ塾のブログ



球の表面積と体積の公式 数学fun


球の表面積の公式の求め方


中学生でもわかる球の表面積の 公式の導き方 セルフ塾のブログ


初等幾何 球の表面積を求める 大人が学び直す数学


微分でつなげる円や球の公式 すうがくブログ 式変形ch



数学講師必見 中学数学でも必須 球の体積 表面積の覚え方と導出まとめ 高校数学 塾講師ステーション情報局



球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



球の表面積の公式について みたにっき はてな



初等幾何 球の表面積を求める 大人が学び直す数学
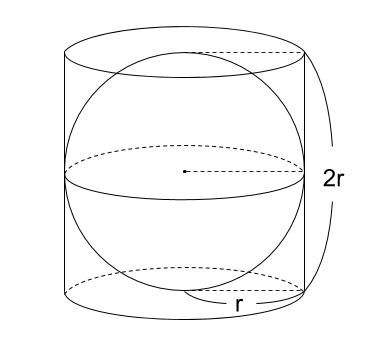


中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
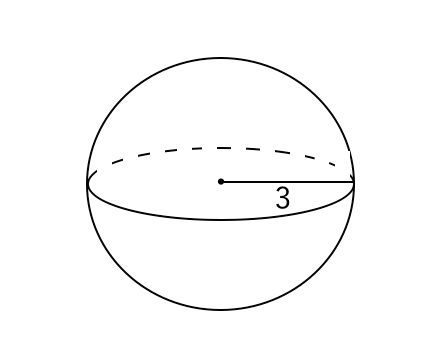


球の表面積と体積の求め方 苦手な数学を簡単に



Newtonライト 円周率p ニュートンプレス



中1 数学 6 5 球の体積 表面積 Youtube



中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく


研究


図形に強くなる なぜ 立体図形 は難しい 中学受験ブログ



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
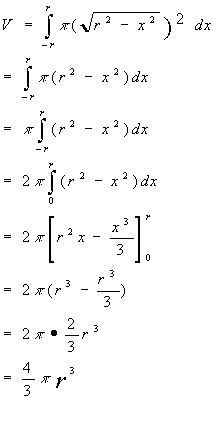


壮大 球体 の 体積 の 求め 方 公式 壁紙 配布


Mathematics 球の体積と表面積を求める公式 働きアリ



球の表面積と体積の公式 数学fun


円と球の求積 直感的方法



球体の表面積 中学生に分かるように真剣に考えてみた うちーノート


大学入試問題


球の体積と表面積を積分で証明 高校数学の美しい物語



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ



球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ


数学の球の体積 表面積についてです 今日 なぜ球の体積は4 3pr3乗になる Yahoo 知恵袋


例題対比 球の体積と表面積



何故abcdの体積は4vに等しいと言えるのですか 高校数学に関する質問 勉強質問サイト



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ


数学 球の表面積を積分で計算してもうまくいかない人へ



球の体積と表面積 Jsciencer


数学 球の表面積を積分で計算してもうまくいかない人へ



球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



Mathematics 球の体積と表面積を求める公式 働きアリ



中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su


研究



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ


優雅 球体 表面積 求め 方 壁紙 配布



173 1 なぜ微分するんですか 教えてください Clear



球の体積の求め方 公式の覚え方と計算方法まとめ 中学数学 理科の学習まとめサイト



球の表面積と体積の公式 数学fun


球の体積が4 3pr 2になる証明を中学生にわかるレベルで教え Yahoo 知恵袋
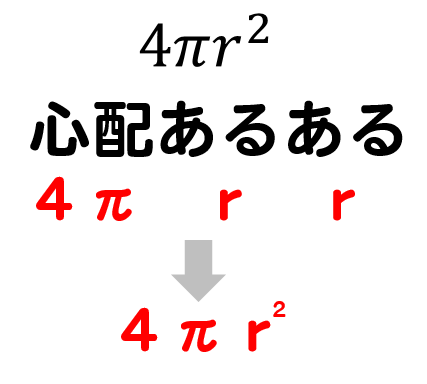


球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ
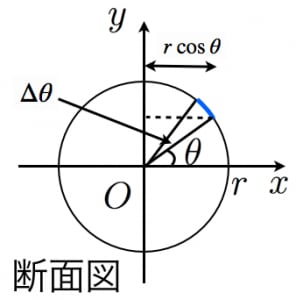


球の体積と表面積を積分で証明 高校数学の美しい物語



球の表面積の求め方 その3 感じる科学 味わう数学



球の表面積と体積の公式 数学fun



球体の体積 中学生に分かるように真剣に考えてみた うちーノート



円の面積 球の体積公式の証明 理系ノート



中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく
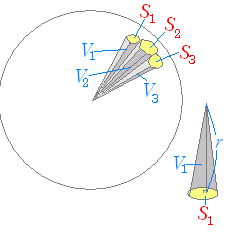


例題対比 球の体積と表面積



球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学


球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス


球の表面積の公式の覚え方 使い方を教えます スタモ 受験 入試 学習の総合サイト



球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張
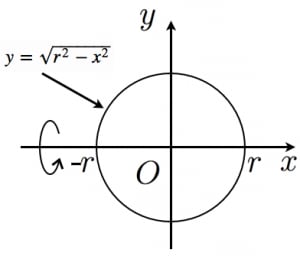


球の体積と表面積を積分で証明 高校数学の美しい物語



簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく



球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく



球の体積を微分すると表面積に 円の面積を微分する円周になるのはなぜか いぬおさんのおもしろ数学実験室



球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく



球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典


球の表面積の公式の求め方



球の体積の求め方でなぜ3分の4が出てくるのかわかりません 中1でもわかるように説明お Clear



中学数学 なぜ4pr 2で 表面積が求められるのか Youtube



球の体積と表面積 Youtube


球の体積が4 3 表面積が4なのはなぜか教えてください ただし Yahoo 知恵袋



球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



球の体積の公式を積分を使わず導く 中受でも出るかも 兄中学生活



球の体積公式の微分が表面積になっている理由 Youtube



球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館



球の体積と表面積 Jsciencer
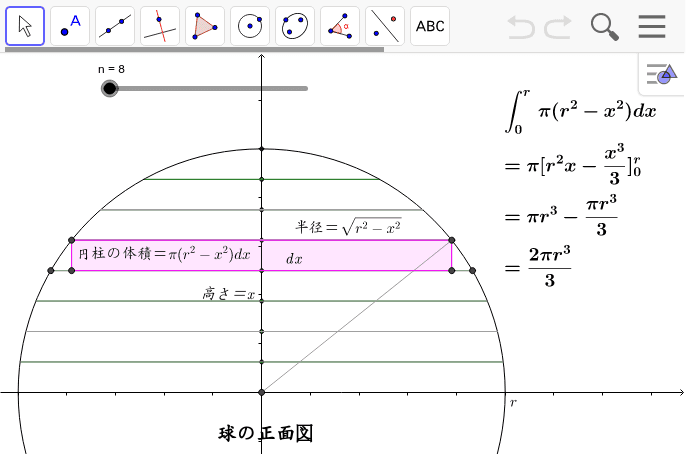


球の体積の積分 Geogebra
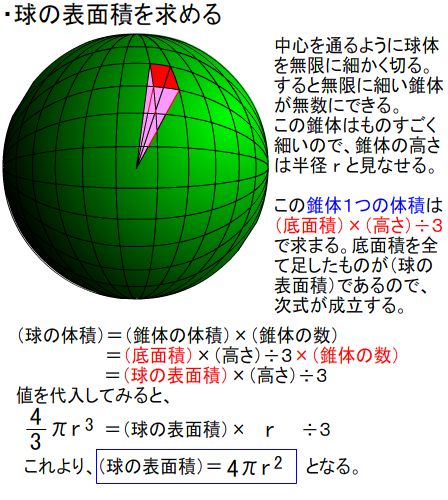


用語与太話 masa ラボ 鸚鵡 オウム の会議は白昼夢 楽天ブログ



球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館



楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ



球の体積と表面積 公式と計算問題と証明 Irohabook



球の表面積と体積の公式 数学fun



3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



球の体積と表面積 公式と計算問題と証明 Irohabook


Mathematics 球の体積と表面積を求める公式 働きアリ



0 件のコメント:
コメントを投稿